贝叶斯网络(BN) 用于以某种方式对包含不确定性的域进行建模。这种不确定性可能是由于对域的理解不完善、对执行给定任务时领域状态的了解不完整、控制域行为的机制的随机性,或者这些的组合。
贝叶斯网络也称为信念网络(belief networks)和贝叶斯信念网络(Bayesian belief networks)。以前,也使用了术语 因果概率网络(causal probabilistic networks)。BN 是由有向链路连接的节点网络,每个节点都附加了概率函数。BN 的网络(或图)是有向无环图(directed acyclic graph, DAG),即没有在同一节点开始和结束的有向路径。
节点(node)表示具有有限状态数的离散随机变量或连续(高斯分布)随机变量(variable)。在本文档中,术语 “variable” 和 “node” 可以互换使用。节点之间的链接表示节点之间的 (因果) 关系。
如果一个节点没有任何父节点(即没有指向它的链接),则该节点将包含一个边际概率表(marginal probability table)。如果节点是离散的,则它包含它所表示的变量状态的概率分布。如果节点是连续的,则它包含它所表示的随机变量的高斯密度函数(通过均值和方差参数给出)。
如果一个节点确实有父节点(即一个或多个指向它的链接),则该节点包含一个条件概率表(conditional probability table, CPT)。如果节点是离散的,则节点的 CPT(或者更一般地说,条件概率函数(conditional probability function, CPF))中的每个单元都包含节点处于特定状态的条件概率,给定其父节点状态的特定配置。因此,离散节点的 CPT 中的信元数等于该节点的可能状态数与父节点的可能状态数的乘积。如果节点是连续的,则 CPT 包含其离散父级状态的每个配置的平均值和一个方差参数(如果没有离散父级,则为 1)以及离散父级状态的每个配置的每个连续父级的回归系数。
下面的示例尝试使所有这些更加具体。
Apple Tree 示例
此示例的问题域是属于 Jack Fletcher 的一个小果园(我们称他为 Apple Jack)。有一天,Apple Jack发现他最好的苹果树正在掉叶子。现在,他想知道为什么会这样。他知道,如果树是干燥的(由干旱引起的),这并不神秘–树木在干旱期间掉叶是很常见的。另一方面,叶子的脱落可能表明患有疾病。
这种情况可以通过图 1 中的 BN 进行建模。BN 由三个节点组成:Sick、Dry 和 Loses,它们都可以处于以下两种状态之一:Sick 可以是 “sick” 或 “not” – Dry 可以是 “dry” 或 “not” – Loses 可以是 “yes” 或 “no”。节点 Sick 告诉我们苹果树处于 “sick” 状态是生病的。否则,它将处于 “not” 状态。节点 Dry 和 Loses 以相同的方式分别告诉我们树是否干燥以及树是否正在失去叶子。
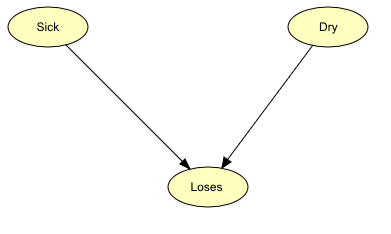
图1:BN代表Apple Jack问题的域。
图1中的BN模拟了从Sick到Loses和从Dry到Loses的因果关系。这体现在两个链接上。
当从节点A到另一个节点B存在因果依赖时,我们预计当A处于某种状态时,这会对B的状态产生影响。在BN中建模因果依赖时应该小心。有时,链接应该指向哪个方向并不十分明显。例如,在我们的例子中,我们说Sick和Loses之间存在因果关系,因为当一棵树生病时,这可能会导致树失去叶子。但是,难道不能说当树失去叶子时,它可能生病了,然后把链接转向另一个方向吗?不,我们不能!是疾病导致了落叶,而不是落叶导致了疾病。
在图1中,我们有BN的图形表示。然而,这只是我们所说的BN的定性表示。在我们称之为BN之前,我们需要指定定量表示。
BN的定量表示是节点的CPT集合。表1、2和3显示了图1 BN中三个节点的CPT。

表 1: P(Sick)

表 2: P(Dry)
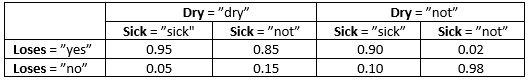
表 3: P(Loses | Sick, Dry)
请注意,所有三个表都显示了节点处于特定状态的概率,这取决于其父节点的状态,但由于Sick和Dry没有任何父节点,表1和表2中的分布不受任何条件的限制。
与给定实例中变量之间的因果关系有关的BN,如上所述,有时被称为静态贝叶斯网络(Static Bayesian Networks,SBN)。SBN只关注当前情况,并不明确地对时间序列进行建模,即忽略过去,不预测未来。例如,在图2中,有两种疾病(D1和D2)可以引起不同的症状(S1和S2)。使用手头的症状信息可以预测每种疾病的概率。
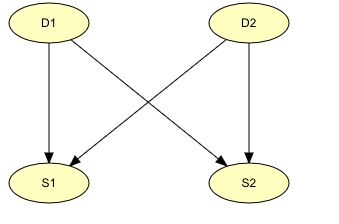
图2:静态贝叶斯网络(SBN)示例
在许多问题域,如上述医疗情况,如果不使用时间维度来表示数据和推理几乎是不可想象的,因为事物会随着时间的推移而演变。SBN,如图2所示,不能用于此类系统,因此必须扩展网络以包含时间信息。这种网络被称为动态贝叶斯网络(Dynamic Bayesian Networks,DBN)。将SBN扩展为DBN的最简单方法是包含SBN的多个实例(时间片)并将它们链接在一起。例如,图3中的网络是通过链接图2中的多个网络实例而获得的。
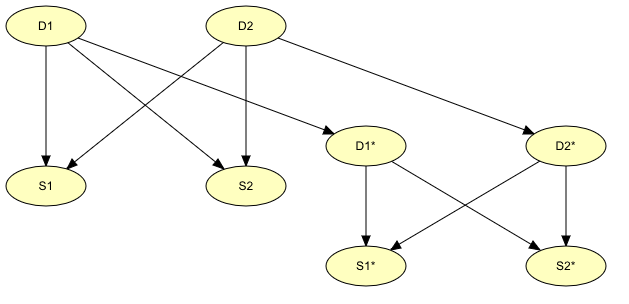
图3:动态贝叶斯网络(DBN)示例
今天疾病的存在将影响明天疾病是否会存在。因此,代表“今天的疾病”(节点D1和D2)和“明天的疾病”的节点(节点D1*和D2*)之间应该存在联系。使用这个新网络,可以预测疾病的进展。
上述示例展示了如何构建非常简单的BNs。当我们构建了一个网络时,我们可以使用它在状态已知的一些节点中输入证据,然后在给定该证据的其他节点中检索计算的新概率。在苹果树的例子中,假设我们知道树正在落叶。然后,我们通过在Loses节点中选择状态“yes”来输入此证据。然后,我们可以将树生病的概率解读为节点sick处于“sick”状态的概率,将树干燥的概率解读为由节点dry处于“dry”状态的可能性。
在给定一些证据的情况下计算其他变量的概率,如上述情况,被称为信念更新(Belief Updating)。另一条可能有趣的信息是,在给定一些证据的情况下,所有随机变量的状态最有可能的全局分配。这被称为信念修正(Belief Revision)。
HUGIN为您提供了一个构建此类网络的工具。在构建了BNs之后,你可以进行信念修正、信念更新等等。如果你正在学习更多关于HUGIN开发环境的知识,现在是学习如何构建BNs教程的好时机。在这里,Apple Tree BN是使用HUGIN图形用户界面构建的。您还可以继续阅读《面向对象网络导论》;例如,在构建具有重复结构的网络时,面向对象的网络非常有用,就像上面的疾病网络一样。或者,您可能希望继续阅读影响图(ID)简介;ID是用效用节点和决策节点扩展的BN。
贝叶斯网络的定义
形式上,贝叶斯网络可以定义如下:
贝叶斯网络是一对(G,P),其中G=(V,E)是有限节点(或顶点)上的有向无环图(DAG),V通过有向链路(或边)相互连接,E和P是一组(条件)概率分布。网络具有以下属性:
- 每个节点代表一个变量A,其父节点代表变量B1、B2、…、Bn(即,对于每个i=1、…、n,Bi,→A),每个节点都被分配一个表示P(A|B1,B2,…,Bn)的条件概率表(CPT)。
节点表示随机变量,链接表示变量之间的概率依赖关系。这些依赖关系通过一组条件概率表(CPT)进行量化:每个变量都被分配了一个给定其父变量的CPT。对于没有父变量的变量,这是一个无条件(也称为边际)分布。
条件独立性
贝叶斯网络的一个重要概念是条件独立性(conditional independence)。如果当变量C的值已知时,关于变量B的值的知识没有提供关于变量A的值的进一步信息,则给定第三组变量C,两组变量A和B被称为(有条件地)独立:
P (A|B,C )=P (A|C )
条件独立性可以直接从图中读取,如下所示:设A、B和C是不相交的变量集,则
- 识别包含其祖先的最小子图;A∪B∪C
- 在具有共同子节点的节点之间添加无向边;
- 所有有向边上的放置方向。
现在,如果从A中的变量到B中的变量的每条路径都包含C中的变量,那么在给定C的情况下,A是有条件独立于B的(Lauritzen等人,1990)。
为了说明这一概念,让我们考虑以下虚构的医学知识
“呼吸急促(呼吸困难)[d]可能是由于肺结核[t]、肺癌症[l]或支气管炎[b],或两者都没有,或不止一种。最近访问亚洲[A]会增加患肺结核的风险,而吸烟被认为是癌症和支气管炎的危险因素。单次胸部X光检查结果[X]并不能区分肺癌和肺结核,呼吸困难的存在与否也没有区别”(Lauritzen&Spiegelholter 1988)。
最后一个事实在图中由中间变量e表示。这个变量是它的两个父变量(t和l)的逻辑或;它总结了一种或两种疾病的存在或两者的不存在。
图4显示了知识的模型。
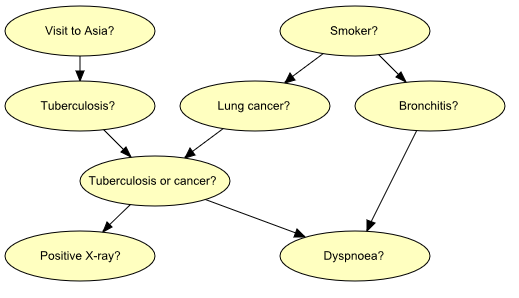
图4:表示肺部疾病医学知识结构方面的图表。
如果我们了解到患者是吸烟者,我们将调整我们对肺癌、癌症和支气管炎的看法(增加风险)。然而,我们对结核病的信念没有改变(即,在给定一组空变量的情况下,t有条件地独立于s)。现在,假设我们为患者获得了阳性的X射线结果。这将影响我们对结核病和癌症的信念,但不会影响我们对支气管炎的信念(即,在给定s的情况下,b条件独立于x)。然而,如果我们也知道患者患有呼吸急促,X射线结果也会影响我们对支气管炎的看法(即,在给定s和d的情况下,b不是有条件独立于X的)。
这些(in)依赖关系都可以使用上述方法从图1的图中读取。
另一种确定条件独立性的等效方法是d分离。,归功于Pearl(1988)..
推论
贝叶斯网络中的推理意味着在给定其他变量的信息(证据)的情况下,计算某些变量的条件概率。
当所有可用证据都是关于感兴趣变量的祖先变量时,这很容易。但是,当有关感兴趣变量的后代的证据可用时,我们必须执行与边方向相反的推理。为此,我们采用贝叶斯定理:
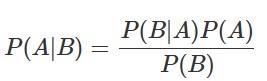
HUGIN推理本质上是贝叶斯定理的巧妙应用;细节可以在Jensen等人(1990(1))的论文中找到。。
具有条件高斯变量的网络
HUGIN决策引擎能够处理具有离散和连续随机变量的网络。连续随机变量必须具有高斯(也称为正态)分布,条件是父变量的值。
具有离散父项I和连续父项Z的连续变量Y的分布是(一维)高斯分布,条件是父项的值:
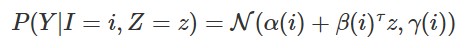
请注意,均值与连续父变量呈线性关系,方差与连续父变量无关。然而,线性函数和方差都可以依赖于离散的父变量。这些限制确保了精确的推断是可能的。
请注意,离散变量不能有连续的父变量。
图5显示了废物焚烧炉的网络模型(Lauritzen 1992):
“由于进入废物[W]的成分差异,废物焚烧炉的(粉尘和重金属)排放量不同。另一个重要因素是废物燃烧方案[B],可以通过测量排放物[C]中的二氧化碳浓度来监测。过滤效率[E]取决于电过滤器的技术状态[F]以及废物[W]中的数量和成分。重金属[Mo]的排放取决于进入废物中的金属[Mi]浓度和一般的粉尘颗粒物[D]排放量。粉尘[D]的排放是通过测量光的穿透性[L]来监测的。”

图5:垃圾焚烧炉模型的结构方面:B、F和W是离散变量,而其余变量是连续变量。
在包含条件高斯变量的网络模型中,推理的结果一如既往地是给定证据的单个变量的信念(即边际分布)。对于离散变量,这相当于变量状态的概率分布。对于条件高斯变量,提供了两种度量:
- 分布的均值和方差;
- 由于该分布通常不是简单的高斯分布,而是高斯分布的混合(即加权和),因此可以获得每个高斯分布的参数列表(权重、均值和方差)。
从图5所示的网络中(假设离散变量B、F和W都是二进制的),我们可以看到
- C的分布可以由最多两个高斯分布组成(如果实例化B,则为一个);
- 最初(即没有证据),E的分布最多由四个高斯分布组成;
- 如果实例化了L(并且没有实例化B、F或W),则E的分布最多由八个高斯分布组成。
另请参阅高斯分布函数部分,了解如何使用HUGIN图形用户界面指定条件高斯分布函数的详细信息。
要了解如何使用HUGIN图形用户界面构建贝叶斯网络,请参阅教程“如何构建贝叶斯网络”。